|
| |
A New Paradigm for High Accuracy Orbit Determination at the
Centimeter Level
by
David W. Allan, Allan's TIME, Inc.
Fountain Green, UT 84632-0066
Neil Ashby, University of Colorado
Boulder, Co 89309
Gus R. German, Allan's TIME, Inc.
Fountain Green, UT 84632-0206
Invited paper presented at
ION GPS 2001
Salt Lake City, Utah
11-14 September 2001

click here for PDF copy (733kb)
NOTE:
If you print out this page, be sure to select "include
images" so that the equations and figures will show.
|
Paper Contents:
Abstract • Introduction •
The Physics Needed and the Concept for this New Paradigm
• Some Practical Considerations • Error Analysis • Clocks • Summary • Perspective • Conclusion
Figures, Table:
Figure
1 -- Doppler • Figure 2 -- Example at GPS Orbit • Figure 3 -- GPS Orbit • Table1
Appendices:
• Appendix A: Navigation and Timing Accuracy at the 30 Centimeter and Sub-Nanosecond Level
• Appendix
B: Review of a New Unified Field Theory
with a New Model of Gravity ( PDF)

Traditionally, satellite positions are determined by earth monitoring
stations and their ephemeredes are given with respect to earth coordinates. As
centimeter accuracies are anticipated we realize that the dynamics of the earth's
variations in spin rate and radius (solid earth tides) are several centimeters
from day to day. A satellite constellation having centimeter accuracy
would provide a robust opportunity to view the earth for the first time from
an independent, local-inertial, reference frame.
Given the recent developments in atomic clocks and other relevant
technologies, a new paradigm is developed herein utilizing currently available
technology. This paradigm leads us to believe that real-time centimeter
accuracies are potentially achievable. This new paradigm takes advantage of
the fundamentals in orbital physics to provide the necessary orthogonality and
independence needed to potentially arrive at the desired robustness and
accuracy, as well as independence for an orbiting constellation.

This paper provides an introduction to the concepts needed to determine
satellite orbits with accuracy on the order of a centimeter and gives an idea of
the fundamental physics involved. The theory has broad applicability, and many
detailed studies would be necessary for any given application. We have used GPS
orbits as an example.
About five years ago the ideas contained herein were conceived, and a patent
application was filed jointly with support from Allan's TIME, Inc, Hewlett
Packard Company, and the University of Colorado. The patent proceedings were
discontinued due to an unusual set of circumstances, and the authors have chosen
at this point in time to share the ideas -- so that they may be more broadly
used. The abstract and the claims for this patent application are listed in
Appendix A as filed some five years ago.
In view of the accuracy desired from the solution, the effects of relativity
must be carefully considered. In the simulations performed in conjunction with
the patent application, the relativity equations were calculated at the
centimeter level. We will briefly discuss other effects that could affect such a
satellite constellation at this level of accuracy.
First, we need the first-order Doppler equation, and we will write it in a
very simple form: y = v/c, where "y" is the normalized,
Doppler-shifted, frequency offset as received at a monitor station coming from
the atomic frequency standard on board a particular satellite (SV),
"v" is the relative velocity between the SV and the same monitor
station clock at a well surveyed point on the earth or otherwise, and c is the
speed of light. Of course, if all the relativity effects are calculated and accommodated
correctly, "y" will be zero when "v" is zero as specified
in the equation. These zero values will occur uniquely at the point of closest
approach -- in principle, providing a fiducial marker for the orbit.
In Figure 1 we show a simple diagram of the effect on this equation when
measuring a Doppler frequency for an observer that is in line with the
frequency of transmission. When the transmitter goes through the observer's
position, two notable things happen: 1) the Doppler shift goes through zero,
and 2) the derivative of the Doppler frequency offset, dy/dt, is a delta
function. These distinctive characteristics of the Doppler transition, allow
it to provide a fiducial marker for that point in time.
We can carry this concept into space with a highly accurate atomic clock on
board a space vehicle (SV). Again, the Doppler frequency will be zero at the
point of closest approach, and this point becomes a fiducial marker for the SV
orbit.
The delta function from our initial case turns into a Doppler frequency
slope, dy/dt, which will be a function of the SV's orbital geometry. As shown
in Figure 2 for a GPS like orbit, this slope is dy = 1 x
10-13 per dt =
175 microseconds. Five years ago, this level of accuracy was easy to achieve.
Now one can do much better. Frequency stability of 1 x 10-14 is commonly
available on the new GPS block 2R rubidium clocks in space.
Next, we may simplistically write Kepler's third law in the following way:
| |
![T^2 = [(4pi^2)/(GMe)]r^3](images/eq-1.gif)
|
(1) |
where T is the period of the orbit, G is the universal gravitational constant,
Me is the mass of the earth, and r is the radius from the center of the
earth to the center of the SV. Now, we recognize in this simplistic
circular orbit that the motion of the spacecraft is orthogonal to the
radius vector. Hence, in Kepler's third law a natural orthogonality is
built into the physics. |
We can now ask the question, using a GPS orbit for example, if we know the
SV's circular position to 175 microseconds out of a period of about 12 hours,
how well do we know the radius vector, r? By taking the derivative of the
above equation, we obtain the following:
| |
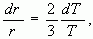
|
(2) |
where we can take dT = 175 microseconds, T is one orbit period of a GPS
SV (about 12 hours), r is the radius vector from the center of the earth
to the SV, and we solve for dr = 7 cm. This value of dr is an
uncertainty on the absolute distance from the center of the earth to the
center of the SV, and is totally independent of atmospheric delay
variations to the extent that they are symmetric about the point of
closest approach. Hence, we see the tremendous leverage factor this
equation provides in determining the radius vector. This is illustrated
in Figure 3. Also, we see that the improvement scales as the accuracy of
the frequency standard in the SV. So if we had an SV frequency standard
with an accuracy of 1 x 10-14, then
dr would be reduced to 7 mm. The technology currently exists to place
this high level of accuracy in space. There are numerous other effects
that need to be accounted for to prevent degradation of this level
accuracy, but in concept one sees the tremendous advantage of this
approach. |
Because of the four dimensional nature of this high accuracy problem, one
also has to deal with the estimations of all six of the orbital parameters the
semi-major axis, the eccentricity, the initial longitude, the angle of
perigee, the inclination angle, and the angle of ascending nodes -- in
addition to the relativistic considerations. At least two monitoring stations
are needed in order to avoid ambiguities in determining these parameters.
In principle, all of the computations could be done in the SV. This would
avoid having to communicate data from several monitor stations on the ground,
which is currently a large segment of the overhead for GPS operation. For practical
reasons, one may chose to perform the computations on the ground and then pass
them up to the SV, or to perform them independently in both locations for
redundancy.
One of the biggest practical considerations is to ensure that Equation l is
valid. From a current science perception, this equation will be valid as long
as the relativistic calculations are performed correctly and if the SV has no
other forces than the gravitational force acting upon it. This can be
accomplished to good approximation by having a "drag free" sensor at
the center of mass of the SV, and then having small trim jets to keep it in a
"drag free" state -- as has been done in other tests and as is
planned for the "Gravity Probe-B" space experiment soon to be
launched.
In Table 1 we have made a preliminary error analysis of the various
contributing factors. We have specifically made an estimate of the theoretical
limit. As can be seen, most of the errors are of the order of a centimeter.
The largest one being the error in the speed up and slow down of the earth's
spin -- causing errors of several centimeters over the course of a day. The
variations in the movement of the earth is, of course, one of the several
measurements that one would like to study from this independent-local SV
inertial frame. By looking at correlations across the constellation, one could
sort out what the earth was doing versus what the errors were in the SV's
positions. The earth rotates, at the equator, a centimeter in 22 microseconds.
This would be resolvable, in principle, with an SV clock having an accuracy of
1x 10-14.
If the drag-free error contribution is given by 1/2 a t2, and
the acceleration error "a" is given by 5 x 10-12 g, then
in order to keep this error at one centimeter, the value of "t"
is about 20,000 seconds -- less than six hours. Hence, the acceleration
detectors would have to be updated about four times per day to contribute no
more than one centimeter to the SV ephemeris error.
In typical satellite tracking, the vertical error component is the most
difficult one to minimize. In this new paradigm, the vertical error component
is the easiest. Currently, the center of the earth is not known with an
accuracy of one centimeter. This new paradigm would significantly assist in
improving the accuracy of this measure.
The atomic clocks that are being used, or that are being considered for
space applications, and that would be useful for this new paradigm approach,
are cesium beam, rubidium gas-cel1, and hydrogen maser designs. We will
briefly touch on what we consider to be the best approach for each of these
three types, picking from the best of the technology that is currently
available.
About a decade ago, Hewlett Packard (Len Cutler, Robin Giffard, and
colleagues) developed a revolutionary commercial, cesium-beam, frequency
standard and clock, the model HP 5071A. As a result of the outstanding
performance of this clock, the primary timing centers throughout the world
have acquired them, and this type of clock now makes up 85 % of the weight of
International Atomic time (TAI) and of the official civil time- (UTC) for the
world. It has extremely high accuracy and typically negligible frequency
drift. This technology has the potential to improve the performance of space
cesium clocks by about an order of magnitude. There is no fundamental limiting
reason why this technology couldn't be utilized in space. This technology
provides outstanding long-term stability of the clocks and is the fundamental
reason why these clocks have such a high weight in international timing. This
same technology is now beginning to make a very important contribution to
avionics positioning -- augmenting GPS. However, the short-term stability
gives some limitation; it is about 6 x 10-12 tau-1/2.
This implies
that one would have to average the frequency for about four days to have an
uncertainty of about 1 x l0-14. There are ways to improve the short-term
stability, and those are being. pursued. Because of the tau-1/2 behavior
of the clock noise, whatever factor of improvement is gained, the square of
that factor will be the decrease in time necessary to integrate to a
particular level. In the above example, if 6 x 10-12 tau-1/2 were divided
by a factor of 3 to a level of 2 x 10-12 tau-1/2 , then it would only
take 1/9th of four days (less than 11 hours -- one GPS orbit) to reach an
integrated level of 1 x 10-14 Fortunately, for this kind of noise (white-noise
FM), one does not need to continuously monitor the time of the clock. In fact,
the optimum estimate of the frequency is given by (x(t + tau)
- x(t)/tau, where x(t) is the time
deviation of the clock at time t. These time deviation measurements could be one orbit apart
if the precision of measurement was not a limiting factor (tau = 12
hours).
The GPS Block 2R rubidium clocks have been engineered to an astounding
level, given the limiting physics associated with rubidium gas-cell
technology. Their short-term stability is about 2 x 10-12 tau-1/2,
which is about an order of magnitude better than most of the SV cesium clocks.
Additionally, the flicker floor is lower than that for cesium -- at about 1 x
10-14. However, as can be expected from the fundamental physics of the
devices, the frequency drift of the rubidium clocks is significantly higher
than that of the cesium clocks. Despite this fact, the frequency drift of the
rubidium clocks has been made remarkably low with very careful engineering.
From the fundamental physics of the c1ocks, one would expect the long-term
stability of the cesium-beam clocks to almost always be better than that of
rubidium gas-cell clocks. The next generation rubidium clocks planned for the
GPS III program have even better short-term stability -- about 7 x 10-13
tau-1/2,
which means that in a single pass (tau = 10,000 s) one
could integrate the clock noise down to a level of 1 x 10-14. This
would be nearly ideal for this new paradigm concept for providing centimeter
level accuracies for the SV orbits. However, the frequency drift would have to
be very carefully calibrated with respect to the monitor station reference
frequency standard, and each of the monitor station frequency standards would
need an accuracy of 1 x 10-14.
Only one hydrogen-maser clock has flown in space. This was the special clock
built by Robert F. C. Vessot and colleagues for one of the finest tests of
special and general relativity that has ever been conducted. The Swiss are
proposing to provide a passive hydrogen-maser clock to be space qualified for
the Galileo program. It will be very interesting to see how this program turns
out. The short-term stability of active hydrogen masers can be made
exceptionally good at about 1 x 10-13 tau-1. This
far out-performs any other commercial clock in the short-term and has some
significant benefits in some applications -- as in the current new
paradigm. However, this is not what is being proposed, and wisely so,
because making a space-qualified, active, hydrogen-maser c1ock with very
reliable long-life performance is no small task. The Swiss proposal is much
more reasonable, but has the disadvantage that the short-term stability is not
nearly as good as for the active maser. It is nominally comparable to the
current GPS block 2R rubidium clocks.
Below we list some of the advantages and needs of this new paradigm.
ADVANTAGES:
There are numerous applications where centimeter accuracy is desired, but
the situation is limited by the accuracies afforded by current system
architectures. GPS, as delivered now in real time, without other corrections,
is pushing hard to approach one meter of accuracy. By differencing and double
differencing the data with respect to known fixed points, which requires
post-processing the data; then centimeter level accuracies are possible. By
making use of this new paradigm and other new technologies now being
developed, real-time accuracies at the centimeter level -- without other
correction factors being needed -- will be possible.
Frequency can be measured more accurately than any other quantity. The
length of the "second" (defined by a unique frequency in the cesium
atom) is the most accurate measurement known to man. This new paradigm takes
advantage of this fact. This new paradigm mitigates to a significant degree
the large problem now facing most satellite tracking systems -- determining
the absolute delay through the atmosphere. This delay is highly variable and
unpredictable and is carrier-frequency dependent. If the uncertainty in this
delay could be circumvented to some degree, this, by itself, would be a
significant advantage. This new paradigm offers this circumvention to a
significant degree.
As an example of current high accuracy measurements, the last six GPS block
2R rubidium clocks have long-term stabilities of about 1 x 10-14.
At this outstanding level of performance, they are all experiencing common
instabilities of about 2 x 10-14, with periods of the frequency
instability of the order of three weeks, and with what appears to be close to
a second harmonic is evident as well. However, it isn't a second harmonic
because it isn't tied to the fundamental period. These observations appear to
be common across the six most recently launched satellites. The searching
question is what could be causing this phenomena? As we approach real-time
centimeter accuracies, these kinds of questions will undoubtedly arise, and
they may have very revealing answers.
This paper was given as a last-minute invited, fill-in
paper to help take the place of those who could not come to ION GPS 2001
because of the horrific attack on the United States on 11 September by
terrorists. Hence, there has not been time to do a full development of the
material herein. It is our desire to give enough information so that the
interested investigator can pursue this new paradigm efficiently and well.
When we performed the investigations for the patent application, relevant
technology had not progressed as far as is now available. The current state of
technology makes this new paradigm even more promising. It is believed by the
authors that pursuing the improved levels of accuracy promised by this type of
approach will greatly benefit the user community and also add significantly
to scientific understanding of questions which were previously unanswerable.

return to text
return to text
return to text
|
ACCURATE
ORBIT ERROR SOURCES
|
THEORETICAL
ERROR LIMITS
|
| EARTH SPIN IRREGULARITIES |
4 cm/12 hrs. |
| POLAR MOTION |
~ cm |
| IONOSPHERE |
~ cm |
| TROPOSPHERE |
~ cm |
| CLOCK FREQUENCY ACCURACY |
< cm |
| CLOCK FREQUENCY STABILITY |
< cm |
| ZERO-g UNCERTAINTIES |
t2 x 2.5 x 10-11 m/s2 |
| GRAVITATIONAL EFFECT OF MOON
|
7 x l0-16
|
| GRAVITATIONAL EFFECT OF SUN
|
4 x 10-17
|
| EARTH TIDES
|
~ cm |
| MULTIPATH |
~ cm |
| RECEIVER DELAY VARIATIONS
|
~ cm |
| MONITOR STATION CLOCK
|
< cm |
| MONITOR STATION LOCATION
|
1 to 2 cm
|
| MEASUREMENT UNCERTAINTIES
|
~ cm |
|
ALTITUDE OF SATELLITE
Involves trade-offs between several
factors: clock noise, integration time, Kepler's 3rd law leverage factor,
geometry of satellites with monitor stations, method of measuring
ionosphere and troposphere and other factors |
~ cm |
return to text

Appendices
• Appendix A: Navigation and Timing Accuracy at the 30 Centimeter and Sub-Nanosecond Level
• Appendix
B: Review of a New Unified Field Theory
with a New Model of Gravity (PDF)
See also
| |
|