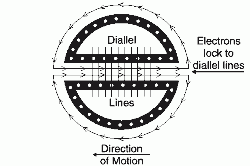
For illustrative
purposes, imagine two semicircles with the diameters together and with the
current circulating in opposite directions in each of the two. Thus, the
current would flow in the same direction along the conducting diameter. If the
electrons could be made to bind to the diallel lines, then they would be
spaced in bundles associated with each line along the diameter -- the diameter
being at right angles to these lines. Bound by the quantum forces, these
bundles of electrons would move with the diallel lines. The return current in
each of the semicircles would be moving rapidly across the diallel lines if,
for example, the diameter is crossing the diallel lines as in a satellite.
If an oscillator could be designed to both sense these pulses and to
balance their movement in order to overcome the resistance in the semicircle
loops, then this oscillator's frequency would be locked to the frequency of
passage of the diallel lines. This would be like a space odometer. If this
oscillator could be locked with no slips, this could, in principle, precisely
map the number of the diallel lines.
Against a good reference-frequency standard, this could yield very precise
information about the mass density of the earth as the density of these lines
changes with the mass density from which they originate. This could allow fine
detailed measurements of changes in these diallel lines due to sub-earth
surface activities -- volcanic, and otherwise. This may also allow a greatly
improved estimate of the higher-order moments of the earth's gravitational
field. Mapping super-earth changes in diallel lines could result from
energy-density changes due to weather storm systems or other man-made
activities.
On the surface of the earth, a highly precise diallel odometer could be
compared with an accurate distance device -- noting changes on an arc along
the face of the earth. Studies along an earthquake fault may allow the
monitoring of stress build up and earth quake prediction. The latter is not
able to be done with any level of confidence at this time.
If the diameters in this electron wheel were a plate, orthogonal to the
diallel lines, with sensors for counting the pulses at the edge of the plate,
this would increase the efficiency and the information. The counter-rotating
loops are necessary to add to zero the EMF contributed by local DC magnetic
fields, and these fields need to be nominally homogeneous for adequate
cancellation of their force effects on the electrons. These loops should
probably be made as small as possible to minimize their cross-sectional area.
In a sophisticated system, the local magnetic fields could be sensed, and the
two loops adjusted to obtain complete cancellation of magnetic field forces on
the electrons.
At GPS orbits, the estimated frequency of the local oscillator would be
about 200 MHz. This seems to be a very do-able experiment. It could be done in
the space shuttle.
Since the diallel field line spacing can be influenced by the energy fields
coming from any of all the sources, this instrument would be very sensitive to
those changes. This proposed instrument would be very useful in designing an
anti-gravity machine -- providing a measurement of one's ability to control
and utilize the diallel gravitational field lines.
In the above, we have assumed that the spacing of the diallel field lines
at the surface of the earth is about 10 micrometers. The first author's
experience with standing numerous eggs is consistent with this value as one
observes the locking range of the egg's built-in servo for causing it to stand
on end.
